근거리장-원거리장 변환법 및 근접 전계 시험

1. 개요
근거리장-원거리장 변환법 (Near field to far field transformation technique, 이하 NF/FF), 또는 Near field scanning은 안테나로부터 근접한 near field 영역에서 측정된 tangential (접면 방향) 성분의 전계 sample 값들을 활용하여 far field에서의 방사 패턴을 알아내는 효율적인 전자장 측정 기법이다. 본 문서는 NF/FF의 원리와 효용성 그리고 활용례에 대해 소개하는 것을 목적으로 한다.
안테나 전파 복사 시 전자기장의 영역은 아래 그림과 같이 세 가지 영역으로 구분되며 일반적으로 각 영역이 구분되는 거리 기준은 전자파의 파장과 안테나의 물리적 크기의 함수로서 설명된다. 각 영역에 대한 정의는 논문이나 책마다 다른데 Balanis 저 'Antenna Theory: Analysis and Design'에 따르면 다음과 같다 [1].

Figure 1. Field region에 대한 분류와 기준 [1]

먼저 안테나와 가장 근접한 reactive near field region의 경우 에너지가 안테나 근방에 머무는 것과 같이 전력이 방사되지 않는 영역이다. 이 영역에서의 전자기파는 공간 상에서 전파되는 propagating wave 뿐만이 아닌 evanescent wave를 포함하며 이 영역에서는 evanescent wave의 영향이 큰 영역이다. evanescent wave는 파의 진행 방향과 에너지의 전달 방향이 다르며 파의 소실이 매질의 loss tangent에 의한 것이 아니라 자연적으로 decaying하는 파인데, Optics에서 다루는 내부 전반사 현상 또한 evanescent wave의 개념으로 설명할 수 있다.
두 번째로 radiative near field region 또는 fresnel region은 reactive field의 영향이 적은 근거리 영역이다. 이 영역에서도 여전히 거리에 따라 안테나 방사 패턴의 변화가 존재하기 때문에 far field region과는 엄연히 구분된다.
마지막으로 far field region 또는 fraunhofer region은 안테나 방사 패턴이 거리에 따라 변화하지 않는 영역이며 far field region에서의 전계는 거리에 반비례하여 1/r로 감쇠한다. 안테나의 특성을 구분 짓는 파라미터 중 하나인 방사 패턴은 거리에 따라 변하지 않는 far field 영역에서 관측점의 방위각과 고각을 변화시켜가며 측정된 패턴으로 정의된다. 또한 전원 근처에서는 구면파 형태를 띠던 파의 양상이 거리가 멀어짐에 따라 곡률이 커지면서 평면 형태에 가까워져 원거리에서는 plane wave의 성질을 띄게 된다.

2. Near field to far field transformation (NF/FF)의 원리
안테나의 방사 패턴은 far field 영역에서 직접 측정되기도 하지만, near field 영역에서 측정된 값을 토대로 analytical method 기반의 계산을 통해 간접적으로 구할 수도 있다. 이때 필요한 것은 near field region에서 측정된 tangential 성분의 전기장의 크기와 위상값이다. NF/FF의 계산 과정은 어떠한 수학적인 근사를 내포하지 않으므로 근거리장 전계 데이터로부터 원거리장 전계를 이론적으로 완벽하게 얻어낼 수 있다. 이때 수집된 near field 데이터 측정 영역의 형태에 따라 planar/cylindrical/spherical로 아래 그림과 같이 세 가지 방식으로 분류할 수 있다. 2차원 평면 상 Δx, Δy 간격으로 분포된 지점들에서 수집된 near field 데이터를 활용할 수도 있고, 원통면 또는 구면 상에서 측정된 데이터를 활용할 수도 있다.

Figure 2. 측정 영역에 따른 NF/FF의 분류 [2]

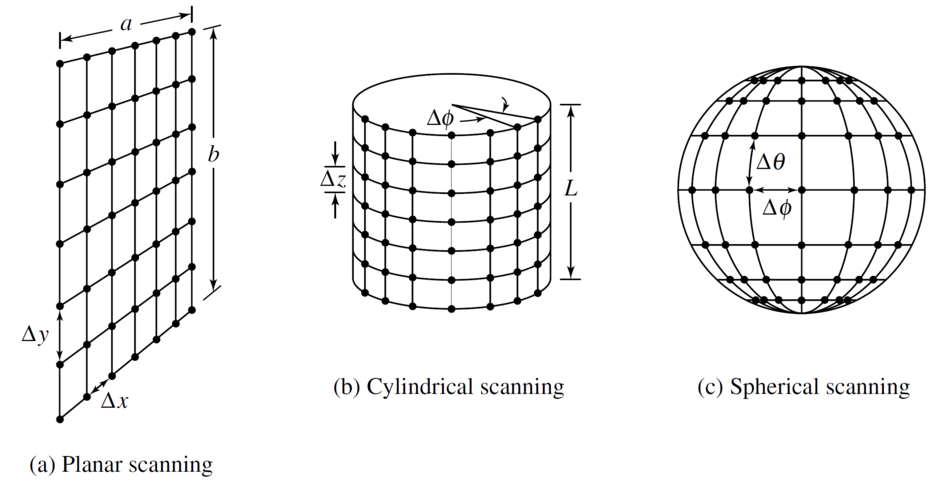
그 중 planar NF/FF 계산 과정에 대해 소개한다. 먼저 near field에서 수집된 전계 Exa, Eya는 아래와 같이 표현된다.

위 식은 임의의 신호를 공간적 푸리에 변환을 통해 나타낸 modal expansion을 설명하는 수식이다. 직관적으로 설명하면 2D 평면 상에 분포된 전계(좌항)는 수많은 다른 방향을 갖는 평면파들의 합(우항)으로서 등가적으로 대체 (superposition) 가능하다는 것이다. 단, 각각의 평면파는 같은 주파수를 가지고 다른 크기를 가질 수 있고 모두 다른 방향(k)을 향한다. Exa, Eya는 각각 전계의 tangential 성분인 x, y성분을 의미하는 것이고 a, b는 샘플링하는 사각형 형태의 근접장 grid의 가로 세로 방향으로의 너비를 뜻한다. Plane wave spectrum fx, fy 는 각 spectral frequency, k를 갖는 평면파를 구성하는 성분의 함량이다. k는 복소수로서 각 평면파들이 갖는 방향에 대한 정보(실수부)와 이에 더해 허수 성분까지 포함하는데, 허수부는 실재하지는 않지만 에너지 관점에서 평면파의 성질을 결정하는 중요한 요소이다. Complex term의 존재 유무에 따라서 각 평면파가 propagating wave가 될지 evanescent wave가 될지가 결정되기 때문이다 [2].

푸리에 변환 식에서 푸리에 계수와 비슷한 역할을 하는 plane wave spectrum fx, fy는 위 식과 같이 계산된다.

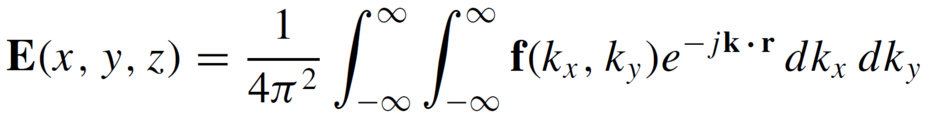
계산된 푸리에 계수를 위 식에 대입하여 적분을 수행하면 최종적으로 임의의 관측점 (x, y, z)에서의 전계의 크기를 구할 수 있다. 그러나 이 식을 직접 계산하고자 한다면 어려움에 맞닥뜨리게 되는데, 정적분 kx, ky의 범위가 -∞~+∞인 복소수로 정의된 값이기 때문이다. 여기서 만약 관측점의 위치를 far field로 제한된다면 계산이 간결해진다. 이는 곧 propagating wave만이 관측점에서의 전계의 크기에 기여하므로 evanescent wave 성분을 일절 무시할 수 있다는 의미이다. far field 상황에서 적용 가능한 method of stationary phase에 따라 kx, ky가 포함된 적분 계산은 관측점과 전원점 간에 이루는 각도와 관련된 함수로 표현되어 아래와 같이 계산이 단순화된다 [2].

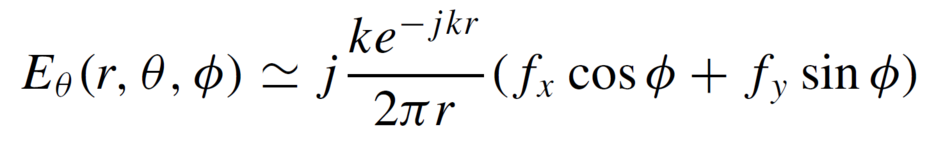
결과적으로 NF/FF 는 near field 영역에서 설정한 2D plane 상에서 측정된 Exa, Eya를 적분하여 공간적 푸리에 계수 fx, fy를 구하고 이를 위의 간단한 근사식에 대입하여 원하는 관측점에서의 far field 데이터를 얻게 되는 과정이다. 원리는 유사하나 cylindrical, spherical NF/FF의 계산에는 bessel function, hankel function of the second kind 등의 함수들이 이용되어 planar NF/FF에 비해 더욱 복잡하며 연산량 또한 많다. planar, cylindrical NF/FF에서는 numerical 적분 연산에 FFT를 쓸 수 있어 계산이 더욱 쉽지만 spherical NF/FF은 FFT를 쓸 수 없다는 치명적인 단점이 있어 다른 두 기법에 비해 연산량이 대폭 증가한다. 다만 planar NF/FF는 안테나와 관측점 사이의 반구 면에서만 복원이 가능하고 rule of thumb으로 대략 15dBi 이상의 고이득 안테나 이용 시에 정확도가 보증되는 반면 spherical NF/FF는 어떠한 안테나 타입에 대해서도 모든 관측점에서의 far field 패턴 예측이 가능하다는 장점이 있다 [3].

3. Near field test의 유용성
그렇다면 왜 far field 패턴을 직접 측정하는 대신 near field를 측정한 후에 수고스럽게 far field로 변환하는 것일까?
첫 번째 이유는 '1. 개요'에서 설명한 far field 기준 거리 확보에 대한 부담을 줄일 수 있다는 것이다. 특히 자동차 레이더와 항공기 레이더와 같이 탑재 플랫폼의 전기적 크기가 크거나 주파수가 낮은 경우에는 far field에 대한 기준 거리가 수십~수백 미터가 되기도 하는데, 이러한 공간 확보는 곧 비용 증가로 이어진다. 시설 부지뿐만이 아닌 전파 흡수체 등 set up 비용도 만만치 않기 때문이다. 곡면 형태의 반사판을 활용하여 plane wave를 인위적으로 형성하여 far field 거리를 단축시키는 Compact range chamber (CATR, CRS) 또한 같은 동기에서 제안된 시스템이다.
둘째로 3차원 방사 패턴 측정 시 소요되는 시간을 줄일 수 있다. 반구 면 상의 방사 패턴을 측정하기 위해서는 고각 방향으로 0˚~180˚, 방위각 방향으로 -90˚~90˚ 범위에서의 측정이 필요하여 1˚ 간격 resolution으로 측정 시 181*181=32,761번의 측정이 필요하다. 반면 near field 측정은 Nyquist sampling theorem에 따라 측정 point 간의 간격이 반 파장 이하가 되도록만 설정하면 완전한 far field 패턴 복원이 가능하다. 아래 사진에 나와있는 planar near field 측정에서는 near field grid 내에서 0.48λ 간격으로 총 52*52 = 2,704 번의 측정으로 빠르고 정확하게 far field 패턴을 얻을 수 있었다. 또한 완전한 far field의 복원이 가능하기 때문에 필요시 1˚ 보다 더욱 정밀한 resolution의 패턴을 얻을 수 있다는 장점이 있다. 특히 Near field test가 최근 더욱 각광받는 이유는 차량용 레이다 또는 5G FR2와 같은 mmWave 대역에서의 활용 사례 때문이다. 거리 감쇠를 상쇄시키기 위한 고이득 빔의 사용이 전제되는 mmWave applications에서는 주관심 영역은 사실상 boresight이기 때문에, 시스템 구성도 간단하고 연산도 빠른 planar NF/FF로도 빔 패턴에 대한 충분한 정보를 얻을 수 있다.

Figure 3. 77GHz 차량용 레이더 성능 측정을 위한 Near field test @ETRI [4]

Figure 4. 조지아텍의 평면형 근전계 시험과 원전계 시험 결과 비교 [2]

이렇듯 NF/FF 측정이 매력적인 이유는 시간적/공간적 비용 측면에서 효율적이면서도 위 figure와 같이 매우 정확한 결과를 얻을 수 있기 때문이다. 위의 figure 4의 결과가 linear scale이 아닌 dB scale인 것을 감안하면 정확도가 어마어마하다는 것을 알 수 있다. NF/FF 결과와 far field 측정 결과 간에 오차가 발생하는 이유는 near field probe와 DUT 간의 interaction/coupling 현상으로 나타는 왜곡에 의한 것이 크며 이러한 왜곡을 보상하는 많은 기법들 또한 연구되고 있다 [2]. 뿐만아니라 planar NF/FF는 수집된 near field grid의 크기(a, b)가 제한되어 있어서 무한 평면 상에서의 모든 전력을 샘플링하지 못하는 것 또한 근본적인 한계이자 오차 발생의 원인이다. 안테나가 바라보는 방향에서 지정 평면 상의 모든 전력을 capture해야 하는데, 지정 평면의 크기를 현실적으로 무한정 늘릴 수는 없기 때문이다. 따라서 안테나 개구면의 크기와 이득 특성에 따라 grid의 크기를 적절하게 조정하는 것이 필요하다. grid 크기 설정, near field 샘플 간의 spacing, probe와 DUT 간의 거리 등과 관련된 사항은 문헌 [5]에 자세하게 설명되어있으나 실제 측정을 통해 어느 정도 경험적으로 감을 잡는 것이 필요하다.
NF/FF는 mmWave 단말의 3D 패턴 측정, 전투기의 RCS 측정, 77 GHz 차량용 레이더 실험 등 다방면으로 이용되고 있다. 국내에도 국방과학연구소 전자전체계단, 만도 ADAS 글로벌R&D센터, 삼성전자 차세대통신연구센터와 같은 다양한 기관들에도 이러한 NF/FF 기반의 근전계 시험 시스템을 갖추고 있다.

4. 결론
NF/FF는 원거리장 측정법 대비 적은 시/공간적 비용으로도 비교적 정확한 방사패턴을 얻을 수 있는 FFT 알고리즘 기반의 효율적인 측정 기법이다.
NF/FF 컨셉을 처음 접했을 때의 충격은 지금도 잊혀지지 않는다. 안테나 주변 가까운 영역을 보고 그 이후 멀리 퍼져나가 먼 거리에 형성되는 장을 예측한다는 것, 그것도 아무런 수학적 근사도 없이 거의 완전하게 예측이 된다는 것은 정말 놀라웠다. 마치 역사 공부를 열심히 하면 매우 적은 오차로 미래를 내다볼 수 있다는 말과 비슷하게 다가왔다. 여러 문헌들에서 NF/FF를 설명할 때 예측(prediction)이라는 표현을 사용하는데, 이미 정해져있던 값을 구해낸다는 관점에서 오히려 복원(reconstruction)이라는 단어가 더 어울리지 않나 싶은 생각이 든다.

References
[1] en.wikipedia.org/wiki/Near_and_far_field
[2] Glenn S. Smith, "An Introduction to Classical Electromagnetic Radiation", Cambridge University Press, 1997
[3] Constantine A. Balanis, "Antenna Theory: Analysis and Design". 3rd ed. Hoboken, NJ: John Wiley, 2005
[4] Seongjae Kim and Kangwook Kim, "Numerical Estimation Based on Ray Tracing for Automotive Radar Beam Through Curved Dielectric Slab," IEEE Progress in Electromagnetics Research Symposium (PIERS), 2018, pp. 344-346
[5]"IEEE Recommended Practice for Near-Field Antenna Measurements," in IEEE Std 1720-2012 , vol., no., pp.1-102, 5 Dec. 2012